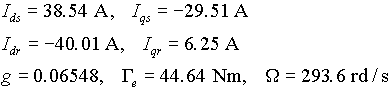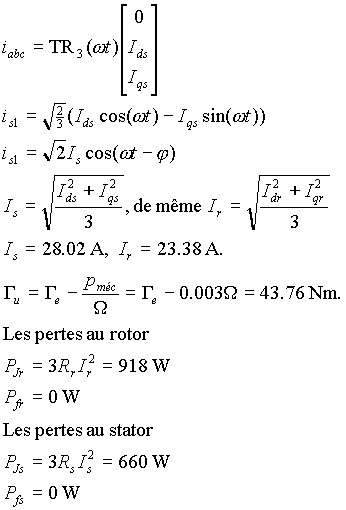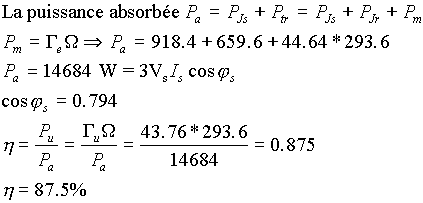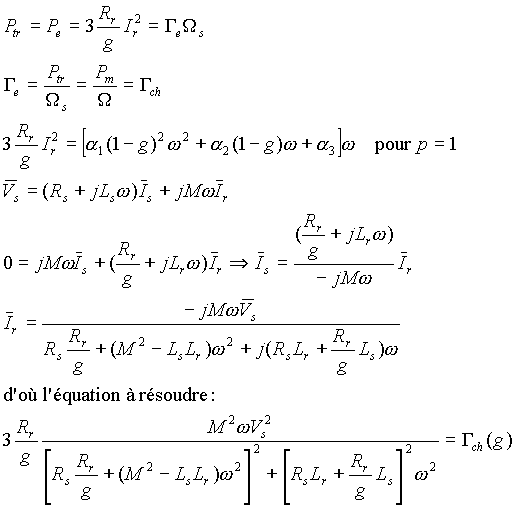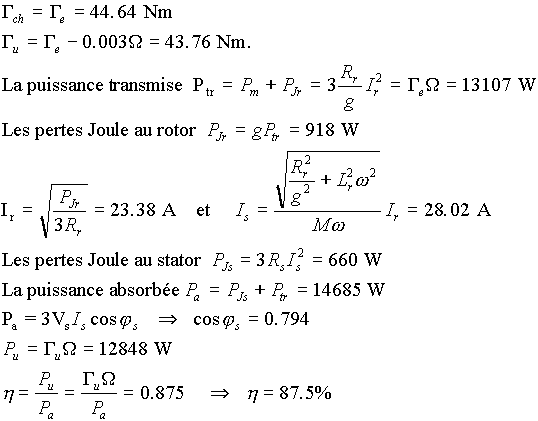BAGHLI Lotfi
DEA PROTEE
INPL
Electrotechnique Analytique
Projet 1
Etude du Démarrage d'un moteur
asynchrone
1 ère
partie : Démarrage
Résumé
Dans ce projet nous nous proposons d'étudier le démarrage
d'un moteur asynchrone. Les équations de la machine sont simplifiées
au moyen d'une transformation de Park adéquate et donnent lieu à
un programme de simulation basé sur deux algorithmes d'intégration.
Cela permet de mettre en évidence l'importance de la méthode
numérique et du pas de calcul de la simulation.
Nous simulons le démarrage à vide puis le couplage à
une charge. Enfin, nous comparons les grandeurs calculées numériquement
en régime permanent et celles obtenues analytiquement.
1. Introduction
Simuler le fonctionnement d'une machine électrique permet sans
grand coût de prévoir son comportement. Que ce soit pour synthétiser
sa commande ou simplement étudier ses régimes transitoires,
il est nécessaire d'avoir un modèle mathématique qui
représente de la meilleure manière la machine. Il faut de
plus y adjoindre la méthode d'intégration numérique
adéquate afin d'effectuer les simulations de fonctionnement et de
connaître la variation des grandeurs électromagnétiques
et mécaniques de la machine.
2. Hypothèses de
travail et caractéristiques de la machine
Nous nous proposons d'étudier un moteur asynchrone à
rotor bobiné à un paire de pôles dont l'enroulement
statorique est monté en étoile.
Nous supposons que la f.m.m. est à répartition sinusoïdale.
Nous négligeons la saturation du circuit magnétique,
l'hystérisis, les courants de Foucault et l'effet de peau.
Nous supposons aussi que les résistances des enroulements restent
constantes. Nous ne traitons que le régime équilibré.
Le système d'alimentation auquel la machine est connectée
à l'instant t=0 est :
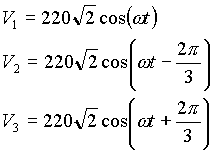
w =100p
Inductances cycliques du stator et du rotor Ls=Lr=0.050 H.
Mutuelle cyclique stator-rotor M=0.0475 H.
Résistance d'une phase statorique Rs=0.28 W.
Résistance d'une phase rotorique Rr=0.56 W
.
Moment d'inertie de la machine J1=0.1 kg m2.
Moment d'inertie total avec la charge J2=0.2 kg m2.
Couple résistant correspondant aux pertes mécaniques
G
r=0.003W Nm.
Couple de charge total ( pertes mécaniques incluses ) G
r=5. 10-4W 2+5. 10-3W
+0.08 Nm.
Le couplage à la charge s'effectue à t1=0.6 s.
3. Mise en équations
Les équations de la machine asynchrone sont données par
:
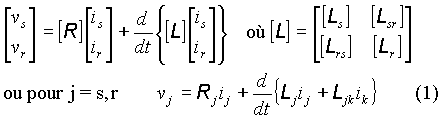
La transformation de park généralisée est le produit
d'une transformation de Concordia et d'une rotation des composants diphasés
:
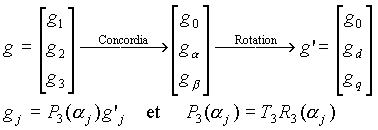
de (1) on a :
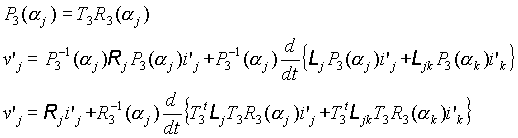
La transformation de Concordia permet d'isoler la composante homopolaire.
De plus, la machine et le système d'alimentation étant symétriques
et équilibrés, cette composante homopolaire est nulle. Nous
ne nous intéresserons qu'aux composantes diphasés.
Soit :
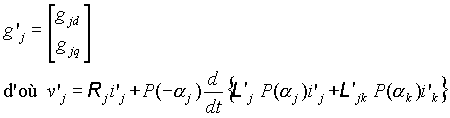
avec
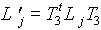
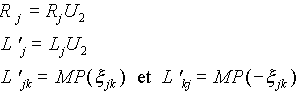
pour j=s,r ,on obtient le système suivant :
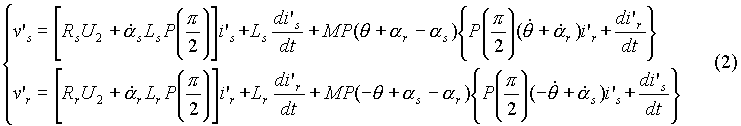
Le couple électromagnétique peut être obtenu à
partir de l'expression de la coénergie
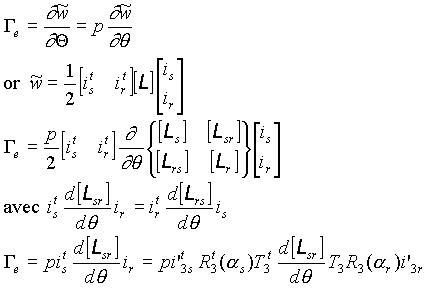
En fait, la composante homopolaire ne participe pas à produire
le couple. De plus, dans notre cas i0s=i0r.
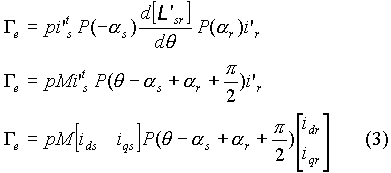
Des expressions (2) et (3), nous remarquons qu'une condition de simplification
est que 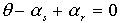 .
.
De plus, en choisissant :
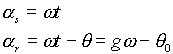
Nous obtenons en régime permanent des grandeurs diphasées
constantes.
Le couple s'écrit alors :
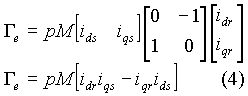
et les équations de la machine :
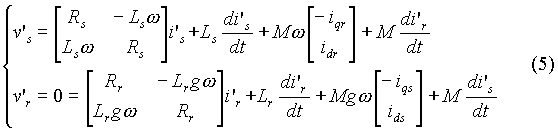
A ces équations électriques, il faut ajouter l'équation
mécanique :
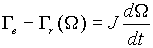
Comme nous choisissons le vecteur d'état du système 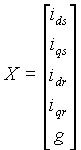 ,
l'équation mécanique peut se mettre sous la forme :
,
l'équation mécanique peut se mettre sous la forme :
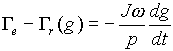
Le système d'équations différentielles à
résoudre est donc le suivant :
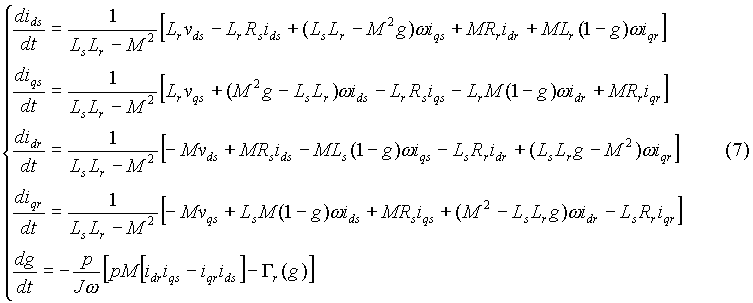
Ce système est non linéaire à cause de la présence
de g dans la matrice A de 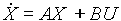 .
.
Avec les conditions initiales : 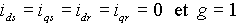 .
.
Pour v's on a :
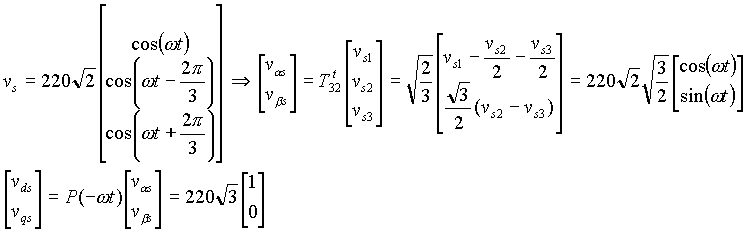
4. Le programme de simulation
Nous avons choisi de programmer en C++. Ce langage offre outre une
bibliothèque mathématique importante ( fonctions en flottant,
double précision et en complexe ), la possibilité de programmer
en orienté objet ( POO ) - que nous utilisons d'ailleurs pour la
gestion des flux d'entrée/sortie -.
Actuellement, le C++ ( nous parlons du Turbo C++ de BORLAND
) donne la vitesse d'exécution la plus rapide avec des possibilités
d'optimisation du code suivant la vitesse ou de la taille du code exécutable
généré. C'est le meilleur langage évolué
disponible sur le marché, il est bien plus puissant et général
que le Turbo Pascal pour ne citer que ce dernier.
Le programme permet de faire l'intégration numérique du
système (7) pas par pas ainsi que la sortie sur fichier des grandeurs
à chaque pas de calcul.
Nous avons choisi d'y inclure deux méthodes numériques;
à savoir la méthode d'Euler modifiée et celle de Runge-Kutta
du 4ème ordre.
· Méthode d'Euler modifiée
:
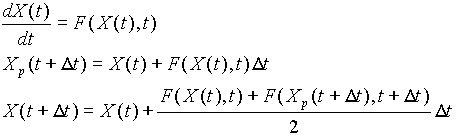
· Méthode de Runge-Kutta du
4ème ordre :
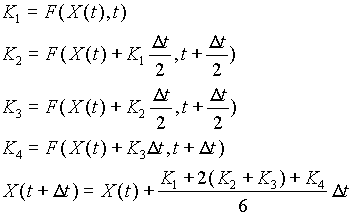
Le programme s'exécute par la ligne de commande suivante :
MAS Graph.dat 1 0.002
où Graph.dat est le nom du
fichier de sortie.
1 désigne la méthode numérique
choisie
-
0 : Euler modifiée.
-
1 : Runge-Kutta du 4ème ordre.
0.002 est le pas d'intégration.
Nous avons développé une procédure ( sous programme
) appelée CalcDX qui calcule le vecteur dérivé dXh
pour un point de fonctionnement donnée Xh. Ses paramètres
étant muets, elle simplifie grandement l'écriture du programme.
La mise en oeuvre de l'algorithme de Runge-Kutta s'en trouve particulièrement
allégée.
Ce programme sort sur le fichier, à chaque pas de calcul, les
courants suivants les axes d, q, le glissement, le courant dans la première
phase statorique, le couple électromagnétique et la vitesse.
A partir de ce fichier, nous traçons les courbes qui nous intéressent.
Le principal problème auquel nous nous sommes heurté dans
l'élaboration de ce programme est l'expression des dXh en fonction
des Xh; il faut être extrêmement vigilant afin de ne pas introduire
d'erreur de signe ou d'indiçage lors de l'établissement de
ces équations et de leur transcription en C++.
| time |
Ids |
Iqs |
Idr |
Iqr |
g |
I1 |
Couple |
Vitesse |
| 0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| 0,002 |
125,9307 |
-38,27827 |
-118,31 |
35,75766 |
0,99998 |
101,5554 |
1,221456 |
0,006126 |
| 0,004 |
183,7764 |
-114,9467 |
-171,1343 |
105,479 |
0,9996 |
135,6289 |
13,62161 |
0,125794 |
| 0,006 |
184,9307 |
-185,5279 |
-172,2901 |
167,1216 |
0,997695 |
97,40868 |
50,28871 |
0,724184 |
| 0,008 |
154,5533 |
-228,3021 |
-147,2838 |
202,4598 |
0,99264 |
7,476167 |
110,8832 |
2,31211 |
| 0,01 |
116,6315 |
-240,3758 |
-118,1838 |
211,5913 |
0,983418 |
-95,22926 |
177,1889 |
5,209315 |
| 0,012 |
87,28941 |
-229,5074 |
-97,75981 |
203,471 |
0,970523 |
-167,8061 |
222,0972 |
9,260424 |
| .... |
.... |
.... |
.... |
.... |
.... |
.... |
.... |
.... |
| .... |
.... |
.... |
.... |
.... |
.... |
.... |
.... |
.... |
| 0,594 |
1,22316 |
-24,22634 |
-0,832936 |
-0,010875 |
0,001283 |
-19,1212 |
0,959135 |
313,7562 |
| 0,596 |
1,222222 |
-24,22631 |
-0,831952 |
-0,01093 |
0,001282 |
-18,50418 |
0,958003 |
313,7566 |
| 0,598 |
1,221344 |
-24,22627 |
-0,83103 |
-0,010981 |
0,001281 |
-10,82001 |
0,956943 |
313,7569 |
| 0,6 |
1,220522 |
-24,22624 |
-0,830167 |
-0,011029 |
0,00128 |
0,996552 |
0,955951 |
313,7572 |
| 0,602 |
1,319848 |
-24,22416 |
-0,935126 |
-0,013174 |
0,002865 |
12,49761 |
1,076826 |
313,2592 |
| 0,604 |
1,580077 |
-24,2135 |
-1,211422 |
-0,023614 |
0,004438 |
19,20128 |
1,395078 |
312,7651 |
| .... |
.... |
.... |
.... |
.... |
.... |
.... |
.... |
.... |
| .... |
.... |
.... |
.... |
.... |
.... |
.... |
.... |
.... |
| 1,394 |
38,53608 |
-29,50643 |
-40,01065 |
6,247236 |
0,06548 |
-32,63584 |
44,6418 |
293,588 |
| 1,396 |
38,53614 |
-29,50645 |
-40,01071 |
6,247259 |
0,065481 |
-13,18967 |
44,64186 |
293,588 |
| 1,398 |
38,53619 |
-29,50647 |
-40,01077 |
6,247281 |
0,065481 |
11,29457 |
44,64192 |
293,5879 |
| 1,4 |
38,53624 |
-29,50649 |
-40,01082 |
6,247302 |
0,065481 |
31,46471 |
44,64198 |
293,5879 |
Tableau 1 : Extrait du fichier de sortie
5. Choix du pas de calcul
Penser qu'il faut prendre  est un raisonnement un peu simpliste. En effet, wt
n'intervient pas directement dans les calculs puisque la transformation
de Park choisie permet de se placer dans le référentiel tournant
au synchronisme. De plus, l'alimentation étant équilibrée,
vds et vqs sont constantes. Ceux qui interviennent par contre, ce sont
les constantes de temps des équations différentielles.
est un raisonnement un peu simpliste. En effet, wt
n'intervient pas directement dans les calculs puisque la transformation
de Park choisie permet de se placer dans le référentiel tournant
au synchronisme. De plus, l'alimentation étant équilibrée,
vds et vqs sont constantes. Ceux qui interviennent par contre, ce sont
les constantes de temps des équations différentielles.
Bien que le système 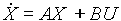 soit non linéaire, il est possible de connaître un ordre de
grandeur de la plus petite constante de temps et donc du pas de calcul
à utiliser.
soit non linéaire, il est possible de connaître un ordre de
grandeur de la plus petite constante de temps et donc du pas de calcul
à utiliser.
Si A est diagonalisable alors 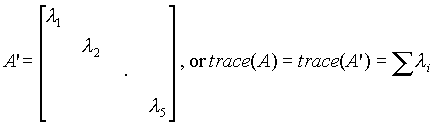
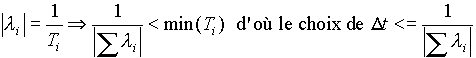
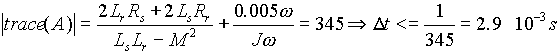 .
.
La méthode d'Euler modifiée est moins précise que
celle de Runge-Kutta du 4ème ordre. En effet, cette dernière
pour un pas de calcul deux fois plus grand ( 2ms ) donne les mêmes
résultats que la méthode d'Euler modifiée à
D
t=1ms.Voir Figure 1. Nous avons donc utilisé la méthode
de Runge-Kutta du 4ème ordre avec un pas de 2ms.
Cependant, les temps d'exécution sont sensiblement proches à
cause du nombre important de sorties sur fichier ( moins de 2s pour un
PC 486 DX 33 ) pour une simulation de 1.4s. Bien que les sorties sur fichiers
soient bufferisées, périodiquement, le buffer ( tampon )
se sature et son contenu est reporté sur le disque. En résumé,
dans notre cas, le temps d'exécution est en grande partie dû
aux écritures sur disque.
6. Variations des grandeurs
Après un régime transitoire d'une durée de 0.2s,
les grandeurs (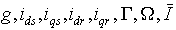 ) varient de
manière exponentielle jusqu'au régime permanent à
vide.
) varient de
manière exponentielle jusqu'au régime permanent à
vide.
A t=0.6s, la machine est couplée à sa charge, toutes les
grandeurs évoluent en exponentielle vers le régime permanent
d'équilibre dynamique qui est pratiquement atteint à t=1s.
Nous constatons que pendant le régime transitoire de démarrage,
le couple comporte une composante pulsante très importante qui engendre
des efforts de torsion considérables.
De même, le courant au démarrage est très important
( 4 fois le courant nominal ), il n'est limité que par l'impédance
interne de la machine à g=1 et comporte des composantes apériodiques.
Nous remarquons sur la courbe i1(t) que le couplage à la charge
est un régime transitoire nettement moins sévère que
celui du démarrage à pleine tension.
7. Régime permanent
Les grandeurs en régime permanent sont :
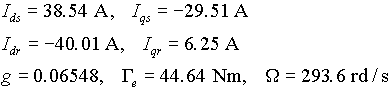
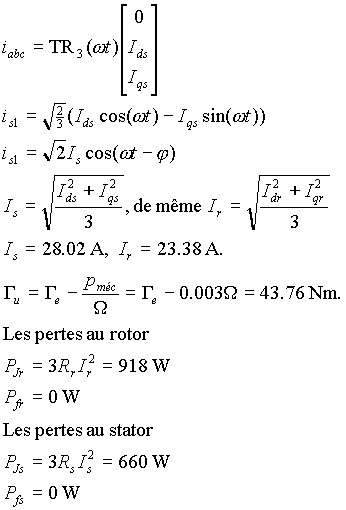
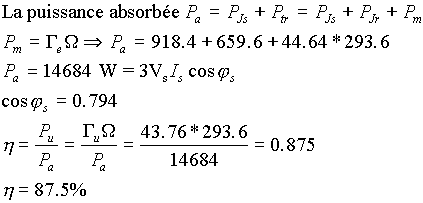
8. Calcul analytique
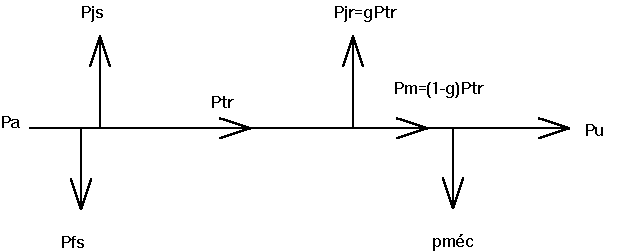
Bilan de puissance
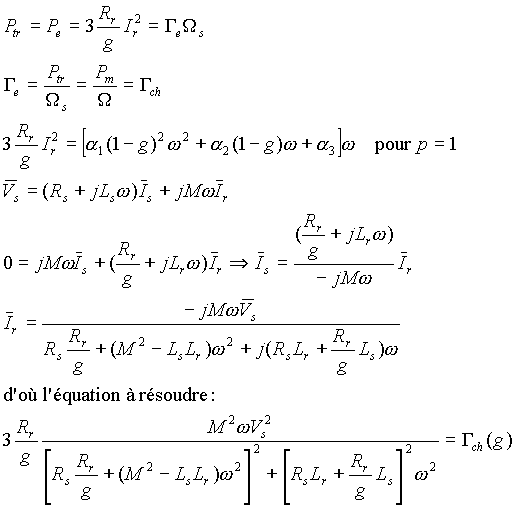
La résolution numérique donne g=0.065485.
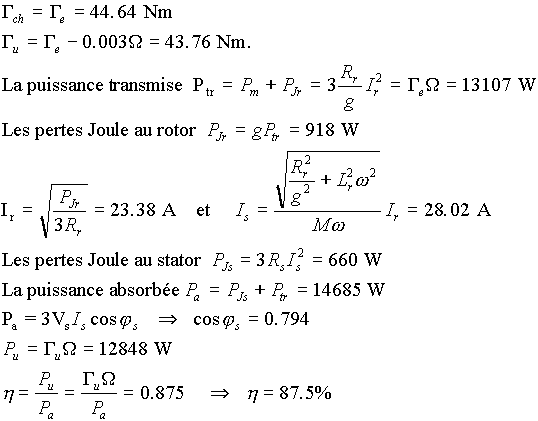
On remarque que les performances calculées
numériquement et
analytiquement sont les mêmes.
Nous avons préféré comparer les résultats
numériques avec ceux calculés analytiquement plutôt
que d'utiliser le diagramme du cercle ( cercle de Blondel ) car, dans notre
cas, les éléments du modèle ( R, L, M ) sont données.
Les équations en régime permanent sont directement exploitables.
Le diagramme du cercle convient surtout quand il est établit pour
une machine réelle à partir d'essais à puissance réduite
, à vide et en court-circuit.
9. Conclusion
Dans ce projet, nous avons mis au point un programme de simulation
du fonctionnement d'un moteur asynchrone avec deux méthodes d'intégration
numérique. Cela nous a permis d'affirmer que la méthode de
Runge-Kutta du 4ème ordre est plus précise que celle d'Euler
modifiée pour un même pas de calcul. Nous avons aussi vu l'influence
du pas de calcul sur la précision des résultats et même
sur la convergence de la méthode. En effet, si le pas de calcul
est trop grand, l'écart entre la courbe réelle et la courbe
calculée se creuse à chaque pas de calcul. Bien que dans
notre cas, le régime permanent ne dépend pas du régime
transitoire, les temps de réponse par contre, n'ont plus aucun rapport
avec les valeurs réelles ( voir figure 1 ).
A cause de la non linéarité du problème, il n'y
a pas de méthode exacte pour déterminer le "bon" pas de calcul,
mais nous proposons une méthode qui permet de l'estimer. Il convient
ensuite de faire plusieurs simulations avec des pas multiples et sous-multiples
afin de s'assurer de la précision des résultats.
Nous remarquons également qu'un démarrage d'un MAS à
pleine tension provoque un appel de courant considérable. D'où
l'utilité d'un rhéostat de démarrage ou mieux une
alimentation variable ( alternostat ). Par contre, une fois que le moteur
tourne à vide, le couplage à la charge ne provoque pas de
surintensité, mais une évolution douce vers le régime
permanent.
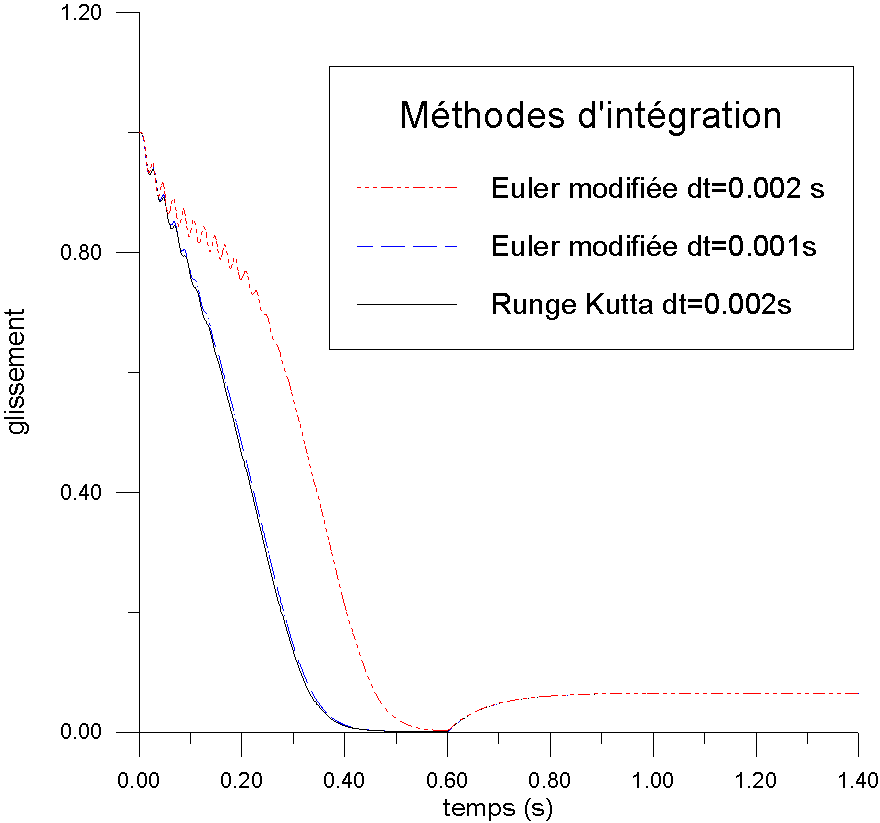
Figure 1
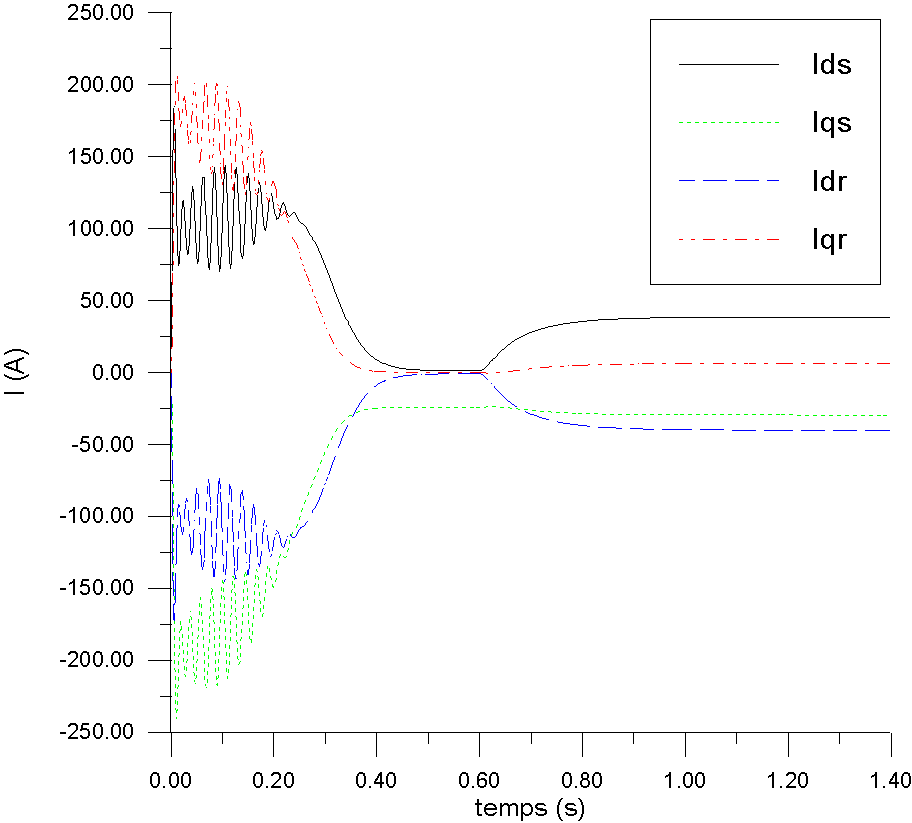
Figure 2
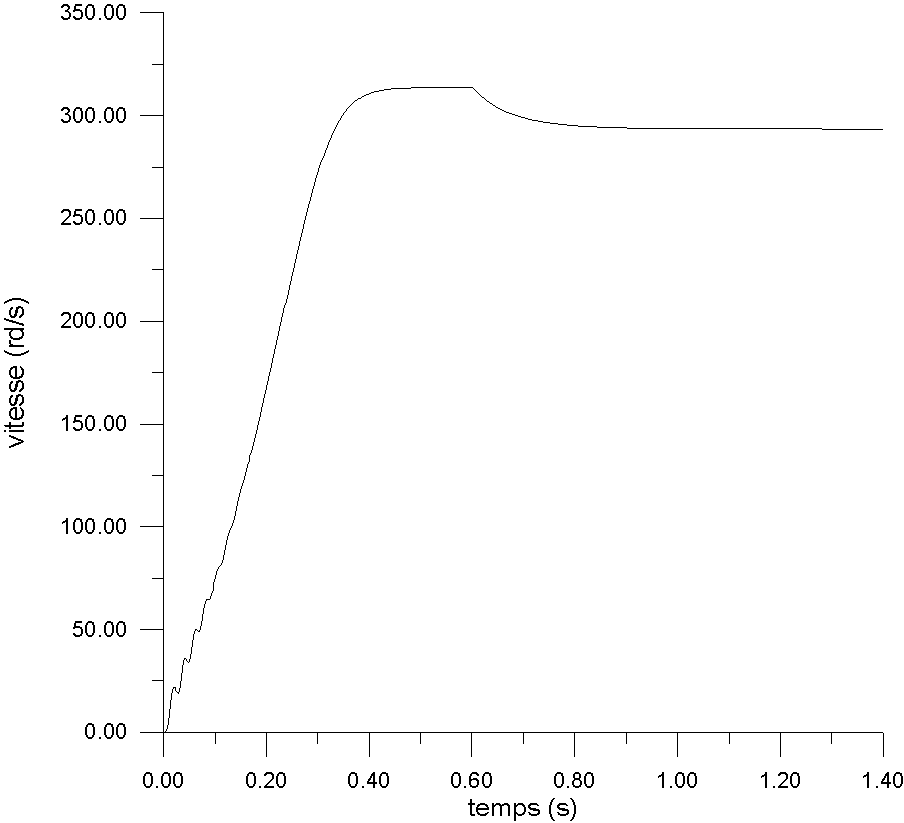
Figure 3
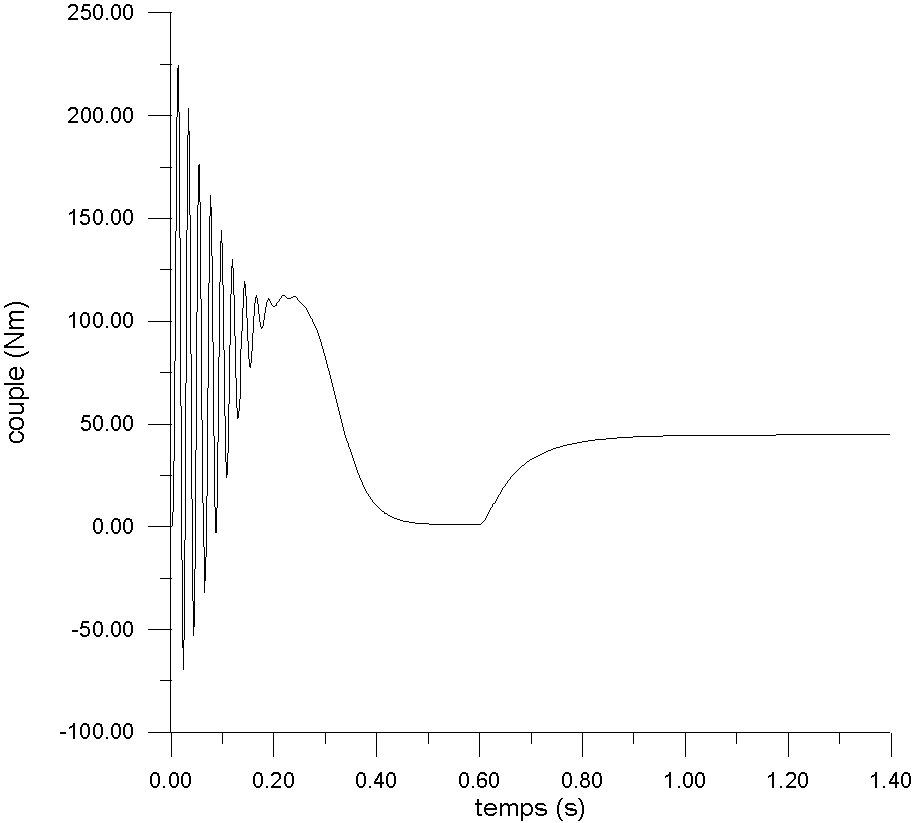
Figure 4
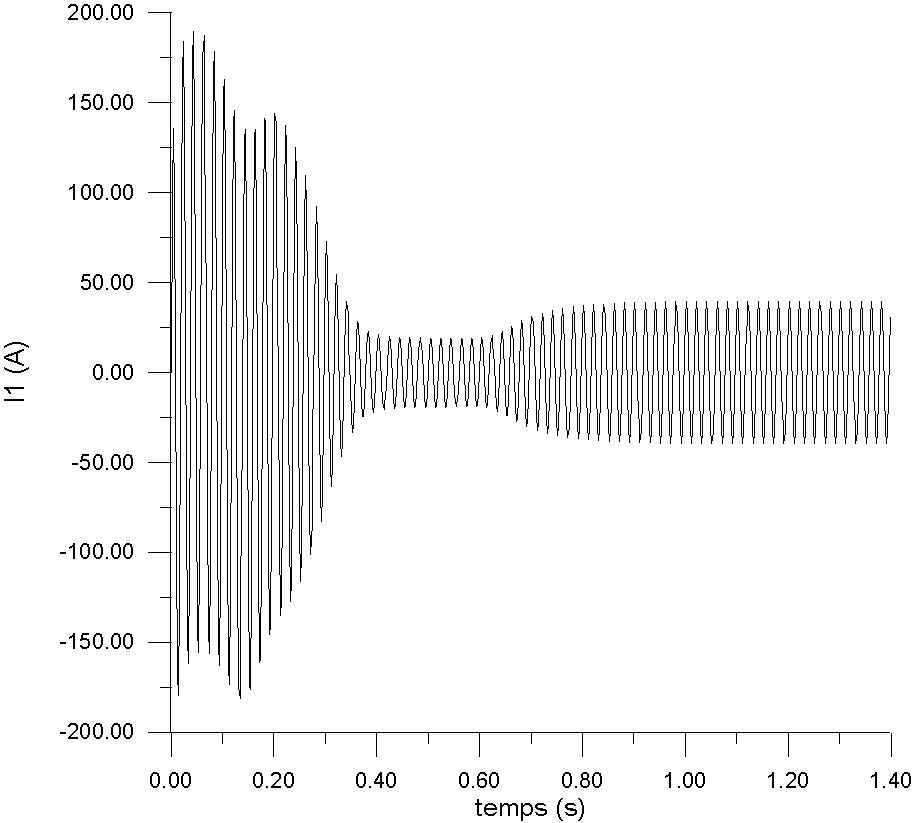
Figure 5
Programme de simulation : MAS.CPP
/*
Programme de calcul du
démarrage d'un MAS
par Lotfi BAGHLI (c)
*/
#include <fstream.h>
#include <string.h>
#include <stdlib.h>
#include <conio.h>
#include <time.h>
#include <math.h>
#include <iomanip.h>
const N=5,
p=1;
const double V=220, W=100*M_PI,
r2s3=sqrt(2./3.),
Rs=0.28, Rr=0.56,
Ls=0.05, Lr=0.05, M=0.0475,
LsLr=Ls*Lr, M2=M*M, LM=LsLr-M2,
J1=0.1, J2=0.2,
a0=0.003, a1=5.e-4, a2=5.e-3,
a3=8.e-2,
t1=0.6, t2=1.4;
int MethodeFlag, Flagt2;
char OutGraphName[81];
double J, t, dt,
Vds, Vqs,
X[N], Xp[N], dXp[N], dXc[N],
K1[N], K2[N], K3[N], K4[N];
ofstream GraphFile;
// routines sortie GraphFile
void OutGraphInit()
{
// justification a gauche !
GraphFile.setf(ios::left, ios::adjustfield);
GraphFile << setprecision(
6) << "time ";
GraphFile << "Ids
"
<< "Iqs
"
<< "Idr
"
<< "Iqr
"
<< "g
";
GraphFile << "I1
"
<< "Couple
"
<< "Vitesse
\n";
}
void OutXGraph()
{
GraphFile <<setw(
6)<< t <<" ";
for ( int i=0; i<N;
i++) GraphFile <<setw( 16)<< X[i] <<" ";
// courant
GraphFile <<setw(
16)<< r2s3*(X[0]*cos(W*t)-X[1]*sin(W*t) ) <<" ";
// couple
GraphFile <<setw(
16)<< p*M*(X[2]*X[1]-X[0]*X[3]) <<" ";
// vitesse
GraphFile <<setw(
16)<< (1-X[4])*W/p <<" ";
GraphFile <<"\n";
}
void OutModif()
{
cout
<< "-- Couplage à la charge à t : "<<setw(
6)<< t << " s\n";
}
// Routine d'attente car sous
Windows, le prompt disparait dès la fin du prog
void WaitKey()
{
cout<< "Pressez une touche
pour continuer\n";
getch();
}
// Initialisation des variables
void Initialisation()
{
for ( int i=0; i<N-1; i++)
X[i]=0;
X[4]=1; // g=1 au démarrage
Flagt2=0;
J=J1;
Vds=V*sqrt(3.);
Vqs=0;
}
// calcul du vecteur dérivé
void CalcDX( double * dXh, double
* Xh )
{
double Gr, Wr=(1-Xh[4])*W;
dXh[0]=( Lr*Vds-Lr*Rs*Xh[0]+(LsLr-M2*Xh[4])*W*Xh[1]+M*Rr*Xh[2]+Lr*M*Wr*Xh[3]
)/LM;
dXh[1]=( Lr*Vqs+(M2*Xh[4]-LsLr)*W*Xh[0]-Lr*Rs*Xh[1]-Lr*M*Wr*Xh[2]+M*Rr*Xh[3]
)/LM;
dXh[2]=( -M*Vds+M*Rs*Xh[0]-Ls*M*Wr*Xh[1]-Ls*Rr*Xh[2]+(LsLr*Xh[4]-M2)*W*Xh[3]
)/LM;
dXh[3]=( -M*Vqs+Ls*M*Wr*Xh[0]+M*Rs*Xh[1]+(M2-LsLr*Xh[4])*W*Xh[2]-Ls*Rr*Xh[3]
)/LM;
if (Flagt2) Gr=a1*Wr*Wr/p/p+a2*Wr/p+a3
;
else Gr=a0*Wr/p;
dXh[4]=-(p*M*(Xh[2]*Xh[1]-Xh[0]*Xh[3])
-Gr )/J/W*p;
}
void main( int NbArg, char *
Arg[])
{
int i;
clock_t start, end;
// initialisation et lecture
cout << "\n\n\tDémarrage
d'un MAS\n";
cout << "\t\tProgrammé
par Lotfi BAGHLI\n";
if ( NbArg!=4) {
cout << "\nvous devez
entrer le nom du fichier de sortie graphique\n";
cout << "ainsi que le
code associé à la méthode d'intégration\n";
cout << "Exemple :
MAS GRAPHOUT.DAT 1 0.002\n";
WaitKey();
exit(1);
}
strcpy(OutGraphName, Arg[1]);
MethodeFlag=atoi( Arg[2]);
dt=atof( Arg[3]);
if (MethodeFlag!=0 &&
MethodeFlag!=1 ) MethodeFlag=1;
if (dt<=0 ) dt=0.002;
cout << "Graph File
: "<< OutGraphName <<"\n";
cout << "\nMéthode
d'intégration : ";
if (MethodeFlag) cout <<
"Runge Kutta ordre 4" <<"\n";
else cout << "Euler
modifiée" <<"\n";
cout << "Pas d'intégration
: "<< dt<<" s\n";
GraphFile.open ( OutGraphName,
ios::out);
if ( !GraphFile) {
cout << "Impossible
to open " << OutGraphName << " file\n";
WaitKey();
exit(1);
}
Initialisation();
OutGraphInit(); // entete du
GraphFile
// le temps initial
t=0.;
OutXGraph(); // sort
donnees pour graph
cout << "time :
"<< t << "\n";
start = clock();
// la boucle principale
do{ // while
( t<=t2 );
if ( t>=t1 &&
Flagt2==0 ) { Flagt2=1;
J=J2;
OutModif();
}
switch (MethodeFlag)
{
case 0 : {
// Euler predictor
CalcDX( dXp, X);
for ( i=0; i<N;
i++) Xp[i]=X[i]+dXp[i]*dt;
// Trapèze
CalcDX( dXc, Xp);
for ( i=0; i<N;
i++) X[i]+=(dXp[i]+dXc[i])*dt/2;
} break;
case 1 : {
// Runge-Kutta
CalcDX( K1, X);
for ( i=0; i<N;
i++) Xp[i]=X[i]+K1[i]*dt/2;
CalcDX( K2, Xp);
for ( i=0; i<N;
i++) Xp[i]=X[i]+K2[i]*dt/2;
CalcDX( K3, Xp);
for ( i=0; i<N;
i++) Xp[i]=X[i]+K3[i]*dt;
CalcDX( K4, Xp);
for ( i=0; i<N;
i++) X[i]+=( K1[i]+2*( K2[i]+K3[i] )+K4[i] )*dt/6;
} break;
}
t+=dt; // incrémente
temps
OutXGraph(); // sort
donnees pour graph
// reboucle
} while ( t<=t2 );
// fin de la simulation : affiche
son temps d'exécution
end = clock();
cout <<
"time : "<< t << "\n";
cout <<"Temps d'exécution
: "<< (end - start)/CLK_TCK << " s\n";
// Ferme le fichier de sortie
GraphFile.close();
WaitKey();
}
Revenir à la page d'accueil
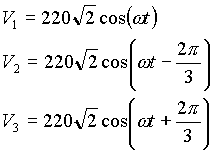
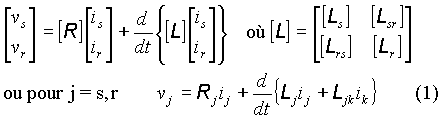
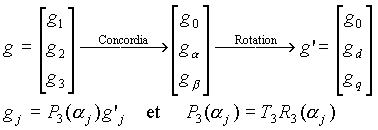
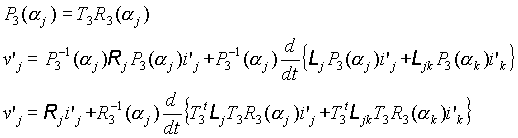
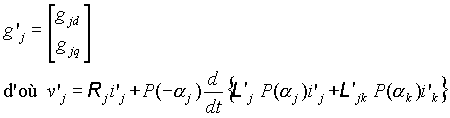
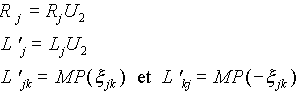
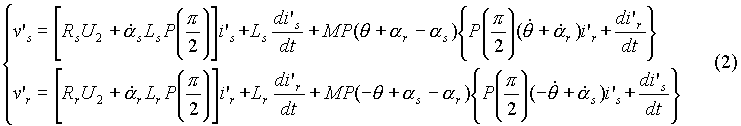
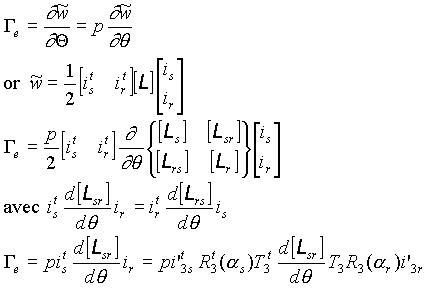
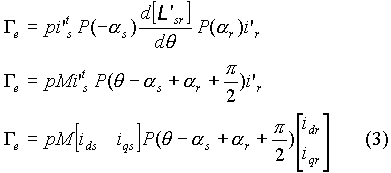
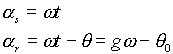
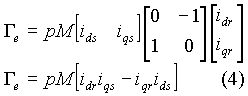
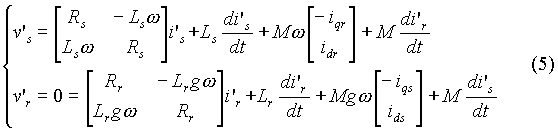
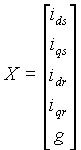 ,
l'équation mécanique peut se mettre sous la forme :
,
l'équation mécanique peut se mettre sous la forme :
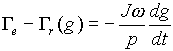
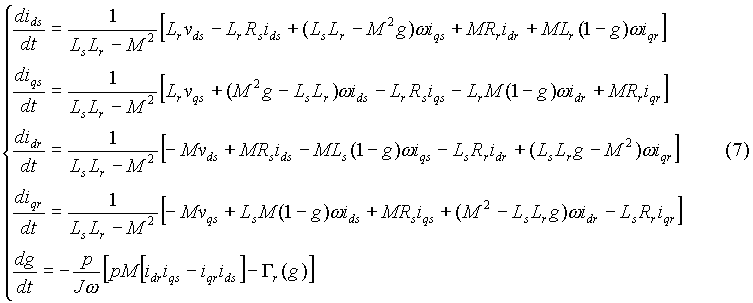
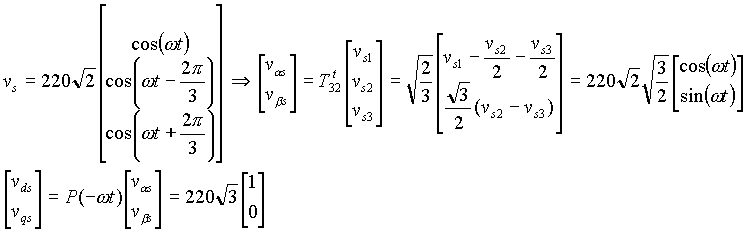
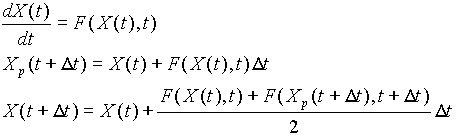
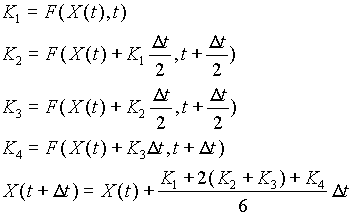
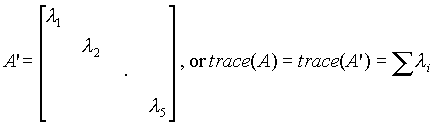
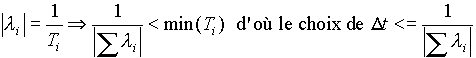
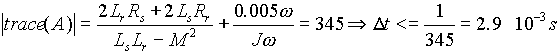 .
.